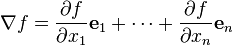以前に<回転のやまとことば>というポストを書いた。数学、物理(ベクトル解析)に限って言えば、英語の<curl>の訳語が<回転>で、<divergence>が<発散>、<gradient>が<勾配>となっている。ベクトル解析の<回転>、<発散>、<勾配>の理解度は人によってまちまちだろうが、物理現象の理解を深めるためには理解度が高い方がいい。その意味では、日本人にとっては、とってつけたような漢語よりやまとことばを使った方がいい場合がある。
勾配(gradient)のやまとことばは<かたむき>だろう。漢字で<傾き>と書くと本来のやまとことばから離れてしまう。<かたむき>の<むき>は<向く>の連用形の体言(名詞)用法。<向く>の動詞的な意味が強く残っている体言(名詞)だ。問題は<かた>の方で、思いつくだけでも
1.向き、方向の<かた>、来(こ)し方
2.片方の<かた>、かたちんば、かたわ(差別用語か?)、片手落ち、片腕、片親
3.方法の<かた>、<やり方>の<かた>
4.形(型)(かたち)の<かた>
5.肩の<かた>
がある。それぞれ違う意味があるがもとをたどれば全て<かた>だ。<かたむき>の<かた>は
1.向き、方向の<かた>
が一番意味がありそうだが、これだと<かたむき>は<向き向き>になってしまうが、<向(む)き>の強調とは違う。<かた向き>と<向き>はちがう。<傾(かたむ)き>、<傾(かたむ)く>には否定的(negative)な意味合いがある。<家、会社が傾(かたむ)く>。いわば暗黙に<下に、下方向に傾く>で、<上に傾(かたむ)く>、<上に傾(かたむ)ける>は変だ。
2.片方の<かた>、かたちんば、かたわ(差別用語か?)、片手落ち、片腕、片親
も否定的な意味があり(足りない、完全ではないの意)、<かたむき>、<かたむく>にはこの意味が混じっていそう。
5.肩の<かた>
<右肩上がり>と言うのが普通だが、<右肩下がり>とも言え、変ではないので、こちらは中立だ。
さて、本題のベクトル解析用語の<勾配>、やまとことば<かたむき>について考えてみる。人にもよるだろうが、もっとも理解しにくいのが<curl、回転>、次いで<divergence、発散>、比較的理解しやすそうなのが<gradient、勾配>だろう。
wiki (日本語版)(2015年9月)の<勾配(ベクトル解析)>の冒頭は次の通り。
”
ベクトル解析におけるスカラー場の勾配(こうばい、英: gradient; グラディエント)は、各点においてそのスカラー場の変化率が最大となる方向への変化率の値を大きさにもつベクトルを対応させるベクトル場である。簡単に言えば、任意の量の空間における変位を、傾きとして表現(例えば図示)することができるが、そこで勾配はこの傾きの向きや傾きのきつさを表している。 ”
wikiの解説は基本的に改善されていくが、正確さの改善も要求されるため、場合によっては、だんだんわけがわからなくなる場合もある。約5年前の2010年10月時の解説は次の通り。
”
ベクトル解析における勾配とは、スカラー場に対して定義され、場の各方向への変化率を記述する偏微分ベクトル(勾配場)のことである。スカラー場からその勾配場を与えるベクトル偏微分作用素そのものをさす
”
これまた人によるが、<偏微分>を知っていれば2010年10月版の方がわかりやすいかもしれない。注意したいのは≪場≫という物理やまとことばが使われていることだ。
2015年9月では
<簡単に言えば、任意の量の空間における変位を、傾きとして表現(例えば図示)することができる、そこで勾配はこの傾きの向きや傾きのきつさを表している。>という表現があり、<傾き>と<勾配(ベクトル用語)>の違いがある。
任意の量は<任意のスカラー量>。<スカラー量>は量だけで方向がない。<変位>はこの場合(スカラー量)は静的な<違い>の意に近い。内容的に肝心なのは
1)任意の量の空間における変位 = 傾き(として表現)
2)勾配(ベクトル用語) = 傾きの向きや傾きのきつさ(を表している)
ベクトルはスカラー(量) と違って<向き(direction)>と<きつさ(magnitude)>。言葉的にも肝心で、<勾配>という漢語を<傾き>、<向き>、<きつさ>というやまとことばを使って説明している。<傾き>なので<きつさ>を使っているが、中立的な語<大きさ>も使われている。
これまた人によるが、勾配(gradient)理解のためには特に
1)任意の量の空間における変位 = 傾き(として表現)
が肝心。変位は明らかに目に見える変化量で理解しがちだが(どれだけ変化したか、どれだけ増えたか減ったか)、解析たるゆえんは変位の(変化)量ではなく、目に見えにくい変位の変化率でとらえることなのだ。ここで<傾き>とは変化率(微分)のことなのだ。さらに<勾配>は<方向付き>の変化率のことなのだ。
したがって、<勾配>とは<方向付き>の変化率の<きつさ(大きさ)>のことだ。やまとことばでは<かたむき>自体の<むき>の意がふくまれているので、<方向付き>の変化率は<かたむき>だけでよさそうだが、残念ながら言葉としては元来<かたむき>自体には肝心な変化率の意はない。いいかえると、
勾配(gradient)= 空間における任意の(スカラー)量のかたむき(と)きつさ(大きさ)
となるが、イマイチだ。変化率は漢語だが、和製漢語のようで、中国では導数が使われているが(wiki China 版)、変化率が関(函)数になる場合は日本でも導関(函)数が使われる。導数も導関(函)数も和製漢語の可能性がある。変化率のやまとことば聞いたことがない。加速度は速度の時間に関する変化率で、<どんどん早く(遅く)なる割合>といえる。<どんどん>は擬態語なので<増す>由来の<ますます>の方がよさそう。<増す>由来とはいえ、<ますます遅くなる>、<ますます減る>、<ますます下がる>はおかしくない。<ますます>は副詞で、普通は変化を示す<増える、減る>、<上がる、下がる>、<速くなる、遅くなる>、<大きくなる、小さくなる>につけて使う。したがって変な日本語になってしまうが、<ますます割合>が変化率に相当するやまとことばの候補だ。したがって
勾配(gradient)= 空間における任意の(スカラー)量の向きごとの<ますます割合>とその大きさ
となる。
堂々めぐりになりそうだが、<割合(わりあい)>はやまとことばだが、<かたむき>と違って、方向性はないので<向き>を加える必要がある。また、<割合>は厳密には<きつさ(大きさ)>そのものではない。したがって<きつさ(大きさ)>を加える必要がある。ただし<割合が大きい、小さい>とは言うので、
勾配 = 空間における任意の(スカラー)量の向きごとの<ますます割合>
でもよさそう。
<割合>の代わりに<具合>、<程度>を使うと<きつさ(大きさ)>はいらないようだ。
勾配(gradient)= 空間における任意の(スカラー)量の向きごとの<ますます具合(程度)>
となる。少しすっきりした。しかし、<具合(ぐあい)>はやまとことばのようだが、<具(ぐ)>は漢語のようで<具合>はいわゆる重箱読みで、半分やまとことばだ。<程度>は漢語だ。<程度>に相当するやまとことばに<ほど>がある。だが<ますますほど>では何のことだかわからなくなりそう。<ますますのほど>はすこしましだ。
個人的には
勾配(gradient)= 空間における任意の(スカラー)量の<向きごとの傾き具合>
が日本語らしい。ただし<傾き>はここでは変化率のこと。タンジェント線(tangent line)(接線)の傾きは変化率を示している。
2010年10月時のwikiの解説を言い換えると(変化率 ->傾き具合)、
”
ベクトル解析における勾配とは、スカラー場に対して定義され、場の各方向への傾き具合を記述する偏微分ベクトル(勾配場)のことである。
”
となる。
----
話はまだ続く。順序が逆になるが、すでに引用したが wiki (日本語版)(2015年9月)の<勾配(ベクトル解析)>の冒頭の冒頭は
”
ベクトル解析におけるスカラー場の勾配(こうばい、英: gradient; グラディエント)は、各点においてそのスカラー場の変化率が最大となる方向への変化率の値を大きさにもつベクトルを対応させるベクトル場である。 ”
で、この後に上で取り上げ、やまとことば解説を試みた<簡単に言えば、任意の量の空間における変位を、傾きとして表現(例えば図示)することができるが、そこで勾配はこの傾きの向きや傾きのきつさを表している。>が続くのだ。これまた数学、物理素人には何のことだかわからないだろう。だが<スカラー場>と<ベクトル場>の<場>は何となくわかるのではないか。ここでの<場>は数学、物理用語だが、砂場、遊び場、工場(ば)、一般的にいえば場所の<場>だが、<場所>と<場>は違う。<場所>は湯桶読みで、重箱読み<具合>と同じく、半分やまとことばだ。<場(ば)>は純やまとことばで一音節のごく簡単な語だが、数学、物理用語としても、また
この場
その場
立ち場
行き場
死に場
のような日常語でも意味は広く、深く、大きい。
これからすると、<場>以外にももっと大和言葉を使えば、この冒頭の冒頭の解説は数学、物理素人にももっとわかりやすくなるのではないか。
-----
以下、勾配(gradient)に興味のある人は読み続けてください。繰り返しになるが、勾配(gradient)の特徴的なのは、
”
ベクトル解析におけるスカラー場の勾配(こうばい、英: gradient; グラディエント)は、各点においてそのスカラー場の変化率が最大となる方向への変化率の値を大きさにもつベクトルを対応させるベクトル場である。 ”
の<点においてそのスカラー場の変化率が最大となる方向への変化率の値を大きさにもつベクトルを対応させるベクトル場>
もっと正確に言うと<変化率が最大となる方向へのその最大の変化率値を大きさにもつベクトル>のところなのだが、残念ながら大体簡単な解説書はこれで済ましてなぜ<勾配(gradient)をとる(ほどこす)と変化率が最大となる方向への変化率の値を大きさにもつベクトル>になるかの説明がないのだが、これは勾配(gradient)理解のうえで不可欠なことだろう。
これはわかってしまえば意外と簡単なのだが、やや詳しい解説書では<方向ベクトル>というのを一旦導入して勾配(gradient)を一般化し、これを直交座標に当てはめる、という回りくどい説明が一般的のようだが、これではまず<方向ベクトル>というのを理解する必要がある。勾配(gradient)数式は
wiki (日本語版)(2015年9月)は一般化した数式もあるが、普通の解説書は
”
式で書けば、勾配は
”
<v>が<方向ベクトル>で<Dv>が<勾配>または<勾配する>を意味している。
続いて
”
直交座標系において、勾配は成分が f の偏微分で与えられるベクトル場
と数学らしい一般化した数式をあげているが、3次元以上は理解しにくいだろう。次いで
”
三次元デカルト座標系においてこれは、i, j, k を基本単位ベクトルとして
............ 。
”
という数式がでてくる。普通の解説書ではこちらがでてくる。ポイントはデカルト座標が直交座標であることなのだが、それとともになぜ足し算になるにかもポイントだ。
sptt